Conectores Lógicos

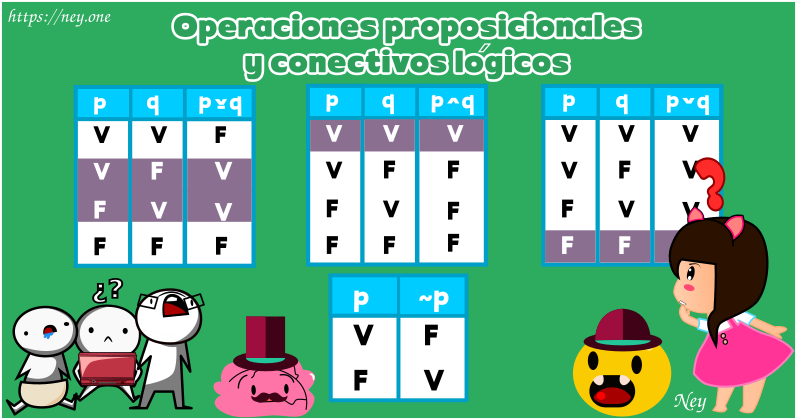
Los conectivos lógicos son enlaces usados para combinar una o más proposiciones, de tal forma que se obtenga como resultado otra proposición llamada compuesta o molecular, cuyo valor de verdad estará determinado por los valores de verdad de las proposiciones que la componen y los conectivos usados.

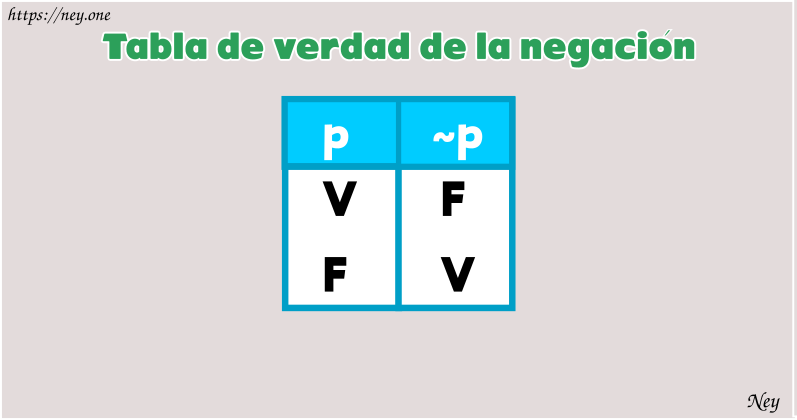
Negación

Es una operación unitaria o monaria, ya que a «partir de una proposición se obtiene otra que es su negación». En otras palabras, la negación de $p$ es la proposición obtenida cuando se antepone la palabra «No» en la proposición $p$ .

Notación: $\neg p, \sim p$

Se lee: «No p» , «No es cierto que p» , «Es falso que p» , «No es verdad que p» .

Ejemplo:

$r$ = El jaguar esta en la selva

$\sim r$ = No es cierto que el jaguar esta en la selva

El valor de verdad de $v(r)= V$ y el valor de verdad de $v( \sim r)= F$

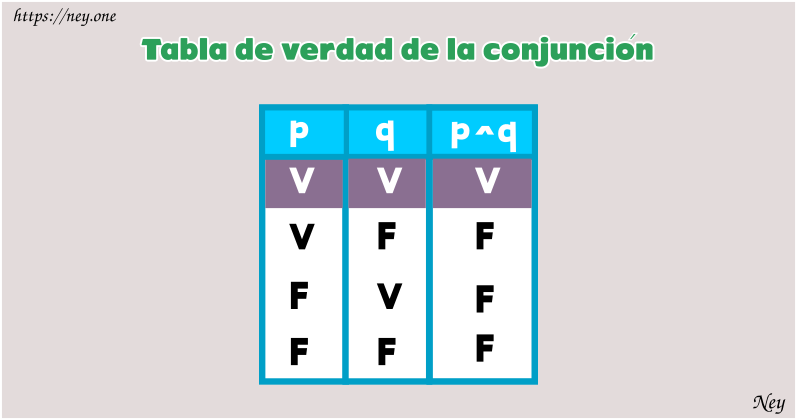
Conjunción

Esta operación es binaria, esto quiere decir que son necesarias 2 proposiciones para efectuar una operación de conjunción, el uso de la conjunción es una proposición compuesta.

«La conjunción sólo es verdadera (V) cuando las 2 proposiciones son verdaderas, en cualquier otro caso es falso (F)» .

Nota: Conjunción es la unión de dos o más elementos y /o cosas.

Notación: $p \wedge q$ , $p$ $\&$ $q$ , $p$ $and$ $q$

Se lee: «p y q» , «p y también q» , «a la vez p y q» .

Ejemplo:

3 es un número impar y 2 es un número primo

$p=$ 3 es un número impar $v(p)=V$

$q=$ 2 es un número primo $v(q)=V$

Por consiguiente: $v(p \wedge q)=V$

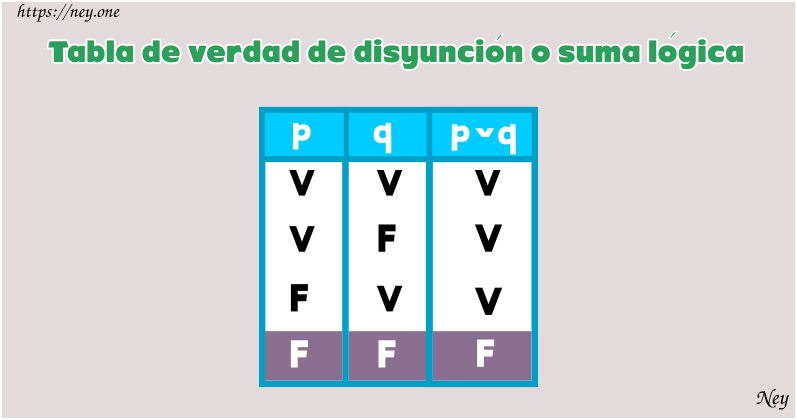
Disyunción inclusiva

Este operador lógico «o» es utilizado en sentido incluyente, ya que «el valor de verdad de la disyunción se da, en el caso de que al menos una de las proposiciones sea verdad (V)» .

La disyunción sólo es falso (F) en el caso en que las 2 proposiciones componentes sean falsas (F).

Notación: $p \lor q$ , $p \text{ o } q$ , $p + q$